Dr. Minah Oh Awarded NSF Research Grant

Dr. Minah Oh from the Department of Mathematics and Statistics has been awarded a National Science Foundation (NSF) research grant to study Efficient Numerical Methods for Axisymmetric Problems. This grant in the amount $100,000 will support Dr. Oh's research and student mentorship for the next two years.

This two-year RUI grant includes funding for summer research students (two students per summer), and they will be involved in constructing efficient antennas that can be used in Hepatic Microwave Ablation, which is a less invasive treatment for various cancers, in addition to the mathematical analysis of the algorithm that they are using in the process. The students will be doing numerical simulations to construct efficient antennas. 

Dr. Oh reports that she is "excited and grateful for this NSF grant that will allow me to focus on the research topics that I have been dedicated to for my entire career." The JMU Department of Mathematics and Statistics is committed to involving students in faculty scholarship, and Dr. Oh's grant will enable students to work alongside her in this mathematical research. "I plan to share my research with as many JMU students as possible and give many of them an opportunity to learn what math research is and to be a part of it. I believe that undergraduate research is one of the many strengths of our department, and I am passionate about making that even more noticeable.” 

Many important real world phenomena can be modeled by using partial differential equations (PDEs), and computer algorithms are used to get a good approximation of the exact solution to such a PDE system. The mathematical analysis of these computer algorithms is very important, since mathematics can be used to prove whether the computer algorithm that is being used will always provide a faithful approximation to the exact solution. The research funded by this NSF grant is on the development and mathematical analysis of efficient computer algorithms that can be used to solve certain PDE systems on axisymmetric domains. 

By using the axial symmetry of a three-dimensional (3D) domain, a cylinder for example, one can reduce the 3D problem into multiple two-dimensional (2D) ones, which results in greatly saving computation time. The resulting 2D problems, however, are quite different from the standard 2D problems, since they are posed in weighted function spaces where the weight function is the radial component r, and the grad, curl, and div formulas for each resulting 2D problem come from a Fourier series decomposition with respect to the rotational variable.  

This project will focus on the construction and mathematical analysis of efficient computer algorithms that can be applied to axisymmetric H(curl) and H(div) problems with applications in various cancer treatments. A new family of finite element spaces constructed by Dr. Oh will be used for this project. This family satisfies the following “commuting diagram property”:

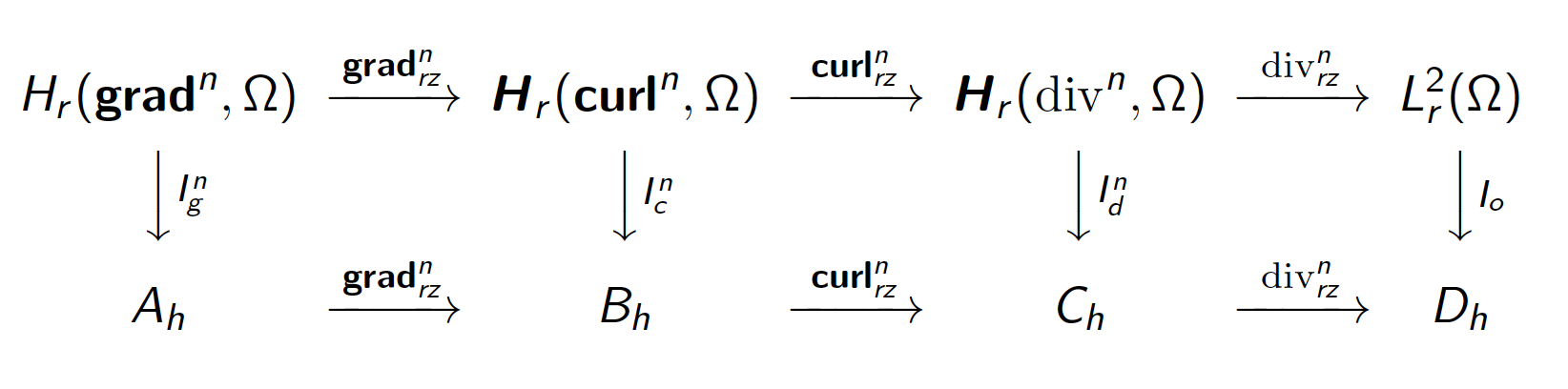
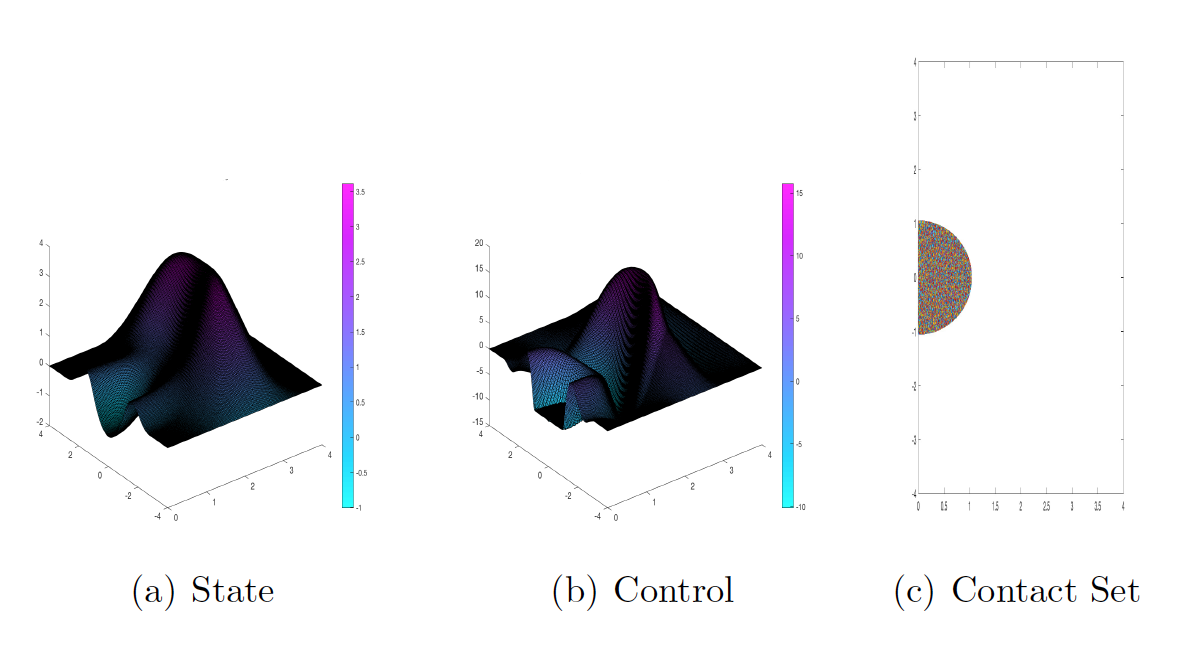
Axisymmetric elliptic optimal control problems will also be analyzed. The following figure depicts the solution of an axisymmetric optimal control sample problem:

Dr. Oh's grant also includes funding to run a “Numerical Analysis Day” for 20 local high school girls where they will learn how math is being used to analyze computer algorithms and also how to program. Students from the JMU Association for Women in Mathematics Student Chapter will be involved in organizing the workshop.